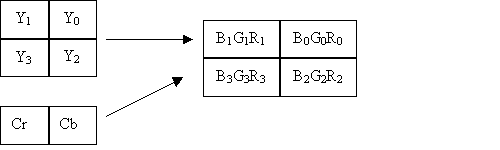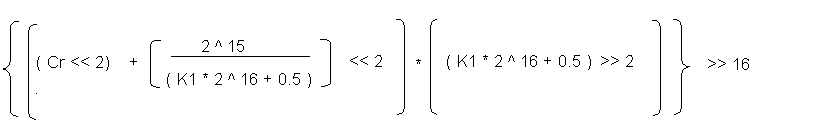1.0. INTRODUCTION

Upsampling and Color Conversion are the final steps in JPEG decompression. Normally these 2 steps are executed independently. Merged Upsampling/Color Conversion can be used when the chroma components in the image are to be upsampled using a simple replication ( i.e. box filtering ). This application note discusses the C implementation of the merged upsample/color conversion in the Independent JPEG Group (IJG) code and shows how performance can be improved by using MMX(TM) technology. Performance results for both the implementations are summarized. The modified MMX technology implementation can be plugged directly into the IJG code base with no code modifications.

2.0. Merged Upsampling/Color Conversion Algorithm

The code for merged upsampling/color conversion (jdmerge.c) in the IJG code base currently provides implementation for YCbCr ---> RGB color conversion and sampling ratios of 2h2v and 2h1v. For other cases we revert back to the general code in jdsample.c and jdcolor.c. jdmerge.c gets executed when the variable master->using_merged_upsample = TRUE in the file jdmaster.c

2.1.1 Color Conversion

Color Conversion is used to convert from the YCbCr ( Y = Luminance, Cb, Cr = Chrominance) color format to the RGB ( R= red, G = green , B = blue) color format. The equations used for doing this are -

R = Y + K1 * Cr

G = Y + K2 * Cb + K3 * Cr

B = Y + K4 * Cb

where K1 = 1.402, K2 = -0.34414, K3 = -0.71414, K4 = 1.772

2.1.2. Upsampling

Since the eye is less sensitive to changes in chrominance as compared to the luminance the JPEG compression subsamples the Cb and the Cr components. In box filtering for 2h2v 2 pixels are taken from 2 adjacent scan lines and they are averaged. The average value is used for all the 4 pixels.

Thus during JPEG decompression the same sample values of Cb and Cr are used for 4 Y values. This helps save work during color conversion by calculating the chroma components just once for a group of 4 pixels.

2.2. C Implementation

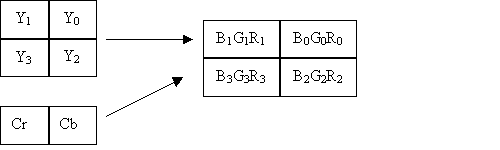
The C implementation of merged upsampling / color conversion precalculates the values of K1 * Cr, K2 * Cb, K3 * Cr and K4 * Cb for all possible values of Cb and Cr and stores it in 4 separate tables ( Cr-R, Cr-G, Cb-G, Cb-B). To avoid floating point arithmetic the fractional constants K1, K2 , K3 and K4 are represented as integers by scaling it up by 2 ^ 16 . The products are divided by 2 ^ 16 with appropriate rounding to get the correct results.

The values of Cb and Cr are read from the image to be decompressed and are used as indices into the pre-calculated tables. These table values are added with 4 Y values ( 2 each from adjacent scan lines) using the equations above to compute 4 RGB pixels. So we have 4 table lookups to compute 4 pixel values.

2.3. MMX(TM) Technology Implementation

Table lookups are costly. To eliminate the cost of table lookups we do the actual calculations in the inner loop using SIMD instructions provided by MMX technology. To avoid floating point arithmetic the fractional constants are again scaled up and represented as integers. In the C version the fractions are scaled up 2 ^ 16. So for example K1 * Cr is represented as -

( ( K1 * 2 ^ 16 + 0.5 ) * Cr + 2 ^15 ) >> 16

Here 0.5 and 2 ^15 are added as the rounding factors. The term ( K1 * 2 ^ 16 + 0.5 ) * Cr can exceed 2 ^16. In MMX we modify the equation so that all the multiplying factors remain under 16 bits. That way we can process 4 data items in parallel using a 64 bit MMX register. We first divide each term in the bracket by ( K1* 2^16 + 0.5 ) and multiply the whole bracket outside by the same. So the equation becomes-

To round off the term 2^15 / ( K1 * 2^16 + 0.5 ) to a whole number we multiply each term inside the bracket by 2^2. . So the above equation becomes -

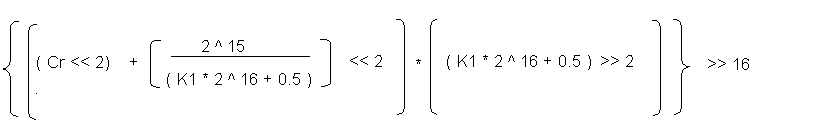
The terms ( 2 ^ 15 / ( K1 * 2 ^ 16 + 0.5 ) << 2 ) and ( ( K1 * 2 ^ 16 + 0.5 ) >> 2) are constants and need not be calculated every time. Also, 16 bit right shift in MMX is avoided by using the PMULHW instruction which returns the upper 16 bits of the product result.

From a higher level the processing of 4 data items in parallel would look something like this-

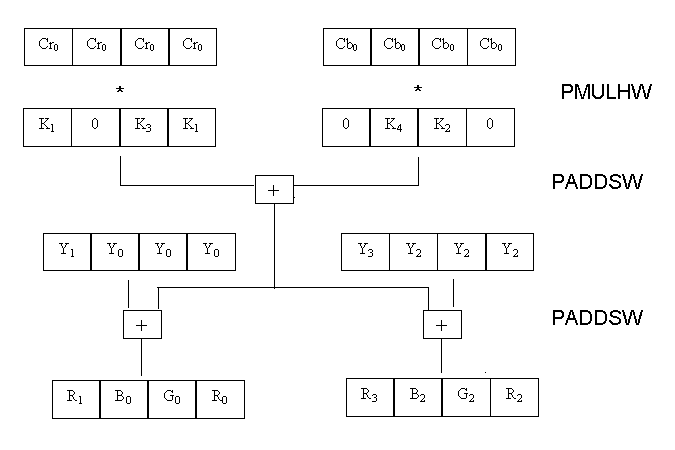
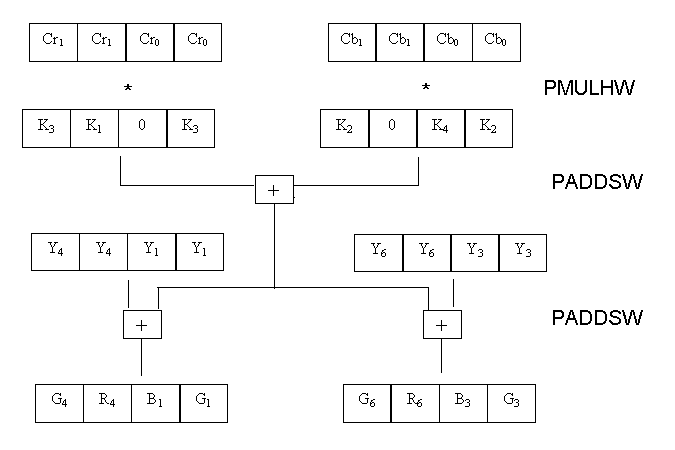
The C implementation calls a macro every time it adds the Y component to the constant * chroma component to clamp the result between 0 - 255. In MMX we can achieve the same with a single PACKUSWB instruction which packs 4 signed 16 bit values from 2 source registers into 8 unsigned bytes in the destination register. It also clamps the values of the bytes between 0 - 255. Thus the call to the macro is eliminated.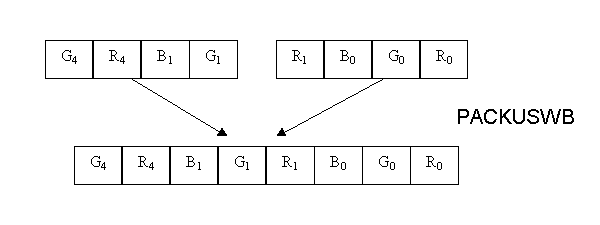

3.0. PERFORMANCE RESULTS

Performance Results were measured on a 266 MHz Pentium II Processor for a 1024 x 768 x 24 bit test JPEG image. The source files were compiled using Microsoft VC++ 5.0 with compiler optimizations set to maximize speed.

4.0. CODE LISTING

Code Listing 1 - C code Implementation of h2v2 for merged color conversion/ upsampling provided by the IJG

Code Listing 2 - MMX Technology Implementation of h2v2 for merged color conversion/ upsampling